Korrelation und Kausalität sind zwei wichtige Begriffe in der Statistik, die oft miteinander verwechselt werden. In diesem Text wird der Unterschied zwischen den beiden anhand von verständlichen Beispielen erklärt und auf die Branche der Unternehmensberatung bezogen. Bedenke, dass nahezu jeder Case innerhalb der Case-Interviews auch dafür genutzt wird deine mathematischen und analytischen Fähigkeiten zu testen.
Korrelation und Kausalität
Das Prinzip der Korrelation
Korrelation beschreibt das Ausmaß der Beziehung zwischen zwei Variablen. Wenn zwei Variablen korrelieren, bedeutet das, dass Veränderungen in einer Variable mit Veränderungen in der anderen Variable einhergehen. Eine positive Korrelation liegt vor, wenn die Werte beider Variablen gemeinsam steigen oder fallen. Ein Beispiel für eine positive Korrelation ist die Beziehung zwischen der Anzahl von Stunden, die man für die Vorbereitung auf eine Prüfung aufwendet, und der erreichten Punktzahl. In der Regel gilt: Je mehr Zeit man investiert, desto besser ist das Prüfungsergebnis (vgl. Quantitative und Qualitative Analysen).
Eine negative Korrelation tritt auf, wenn sich die Werte entgegengesetzt verhalten, das heißt, wenn der Wert einer Variable steigt, fällt der Wert der anderen Variable und umgekehrt. Eine negative Korrelation könnte beispielsweise zwischen der Anzahl der Stunden, die man vor dem Fernseher verbringt, und der körperlichen Fitness bestehen. Je mehr Zeit man vor dem Fernseher verbringt, desto weniger Zeit hat man für körperliche Aktivitäten, was zu einer geringeren Fitness führen kann.
Allerdings ist es wichtig zu verstehen, dass Korrelation allein nicht ausreicht, um auf eine Kausalität zu schließen.
Das Prinzip der Kausalität
Kausalität bedeutet, dass eine Veränderung in einer Variable eine direkte Ursache für die Veränderung in einer anderen Variable ist. Mit anderen Worten: Eine Variable verursacht eine Veränderung in einer anderen Variable. Ein Beispiel, das oft verwendet wird, um den Unterschied zwischen Korrelation und Kausalität zu erklären, ist die Beziehung zwischen der Anzahl der Eisverkäufe und der Anzahl der Sonnenbrände. Es besteht eine positive Korrelation zwischen diesen beiden Variablen, da an sonnigen Tagen mehr Eis verkauft wird und auch mehr Menschen Sonnenbrand bekommen. Es wäre jedoch falsch anzunehmen, dass der Konsum von Eis Sonnenbrände verursacht. In Wirklichkeit ist die gemeinsame Ursache für beides die Sonneneinstrahlung. An sonnigen Tagen kaufen die Menschen mehr Eis und sind auch einem höheren Sonnenbrandrisiko ausgesetzt. Dieses Beispiel verdeutlicht, dass Korrelation nicht automatisch auf Kausalität hindeutet.
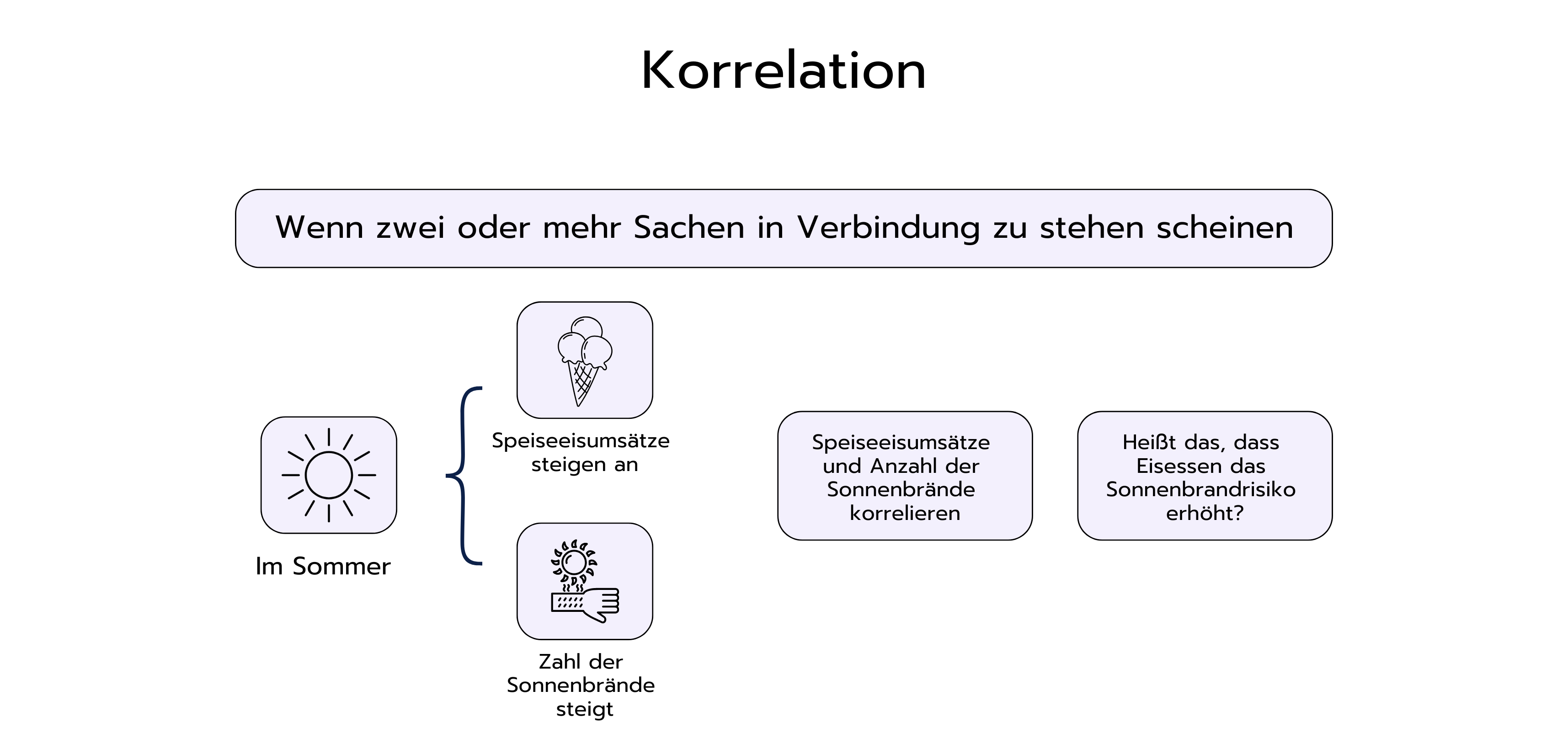
=> Korrelation bedeutet nicht immer Kausalität!
Korrelation und Kausalität in der Unternehmensberatung
Im Bereich Consulting spielt das Verständnis von Mathematik und somit natürlich auch von Korrelation und Kausalität eine entscheidende Rolle. Wenn Berater*innen Daten analysieren, um Unternehmen oder Organisationen zu unterstützen, ist es wichtig, dass sie die richtigen Schlüsse ziehen und keine falschen Annahmen treffen.
Nehmen wir an, ein Unternehmen stellt fest, dass es eine starke Korrelation zwischen dem Einsatz einer bestimmten Marketingstrategie und dem Umsatzwachstum gibt. Das Unternehmen könnte versucht sein, anzunehmen, dass die Marketingstrategie direkt für das Umsatzwachstum verantwortlich ist und daher weiterhin stark in diese Strategie investieren. Allerdings könnte es sein, dass die Korrelation nur darauf hinweist, dass beide Variablen von einer anderen, noch unbekannten Ursache beeinflusst werden. Um die Kausalität zu bestätigen, wären weitere Untersuchungen erforderlich, wie z.B. Experimente oder Kontrollgruppen, um den direkten Einfluss der Marketingstrategie auf den Umsatz zu testen.
Insgesamt ist es wichtig zu verstehen, dass Korrelation und Kausalität unterschiedliche Konzepte sind. Korrelation beschreibt lediglich die Beziehung zwischen zwei Variablen, während Kausalität eine Ursache-Wirkung-Beziehung impliziert. Nur weil zwei Variablen korrelieren, bedeutet das nicht automatisch, dass eine Variable die Ursache für die Veränderung in der anderen Variable ist. Um auf eine Kausalität schließen zu können, sind weitere Untersuchungen und Beweise erforderlich.