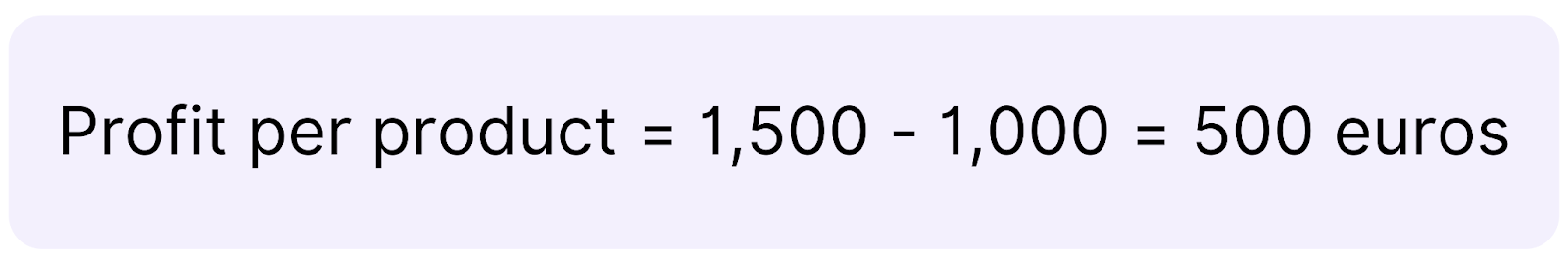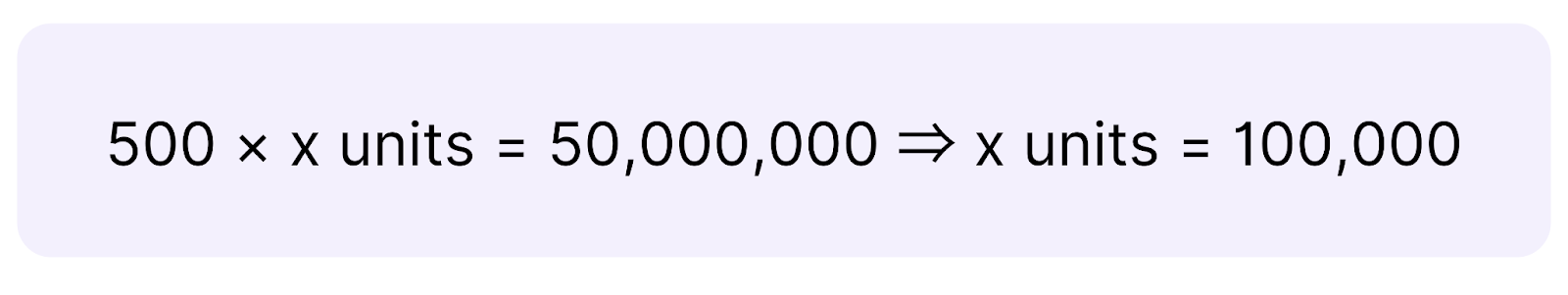The break-even analysis helps you find the point at which a company’s total revenue equals its total costs. This analysis allows you to determine the number of product units that need to be sold to reach profitability, given the product’s price and costs.
🔎 In this article, we’ll show you how to tackle the break-even analysis in a case interview. Enjoy reading!
What is Break-Even Analysis?
A break-even analysis is crucial for assessing a company’s profitability. It illustrates the relationship between profit, revenue, and costs, helping to calculate the break-even point (BEP). It's essential to understand the concept of fixed and variable costs.
👉 Make sure to check out our article on fixed and variable costs!
The formula for calculating the break-even point is:

When fixed costs are greater than zero, it’s critical to have a positive contribution margin per unit (i.e., the price must be higher than variable costs) to reach a break-even point.
Using Break-Even Analysis in Case Interviews
In consulting, break-even analysis is often used to help clients make strategic decisions. Let’s say you’re assisting a company planning to launch a new product. You would analyze the product’s fixed and variable costs to determine the break-even point.
Case Example: Market Entry Strategy in The Lithium Materials Trade Market
Imagine your client is a company entering the lithium material trade. They plan to offer lithium to the electronics industry and face the challenge of identifying profitable price points and associated costs. Your task is to conduct a break-even analysis to find out how many units must be sold to cover initial investments and operating costs.
- The client faces high investment costs for machinery and infrastructure that will be significant in the first few years.
- It’s also expected that the variable costs for raw materials and transport will significantly impact the price per unit.
Step 1: Calculate the Break-Even Point
To find the break-even point, we need the following data:
- Fixed Costs (FC): €500,000 (e.g., rent, machinery costs, salaries)
- Variable Costs per Unit (VC): €100 (e.g., raw material costs, transport)
- Selling Price per Unit (P): €150 (the price at which lithium will be sold)
Step 2: Calculation
Now, let’s plug these values into the break-even formula:
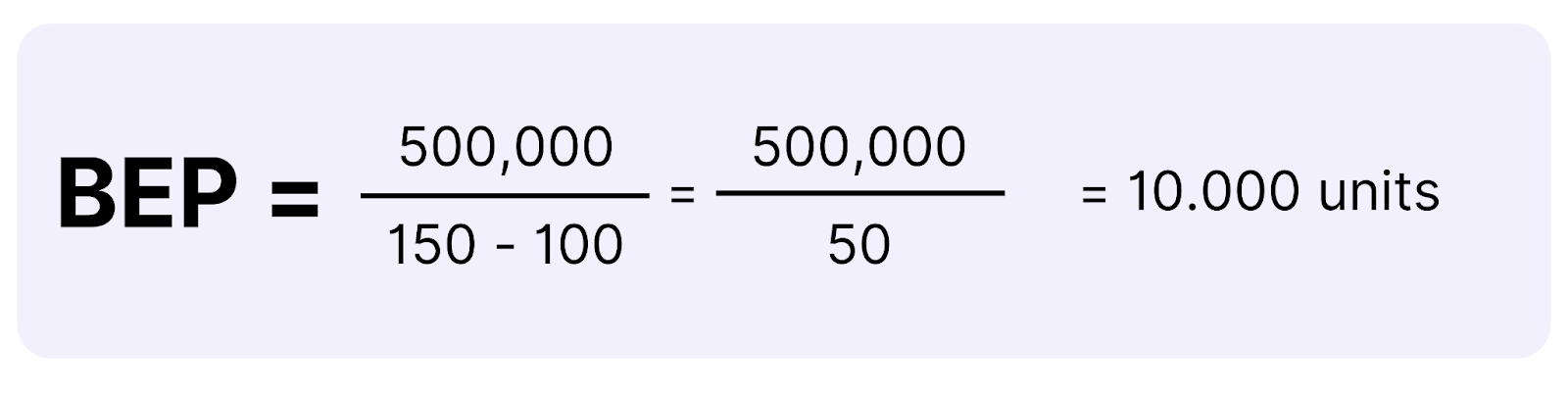
This means the company needs to sell 10,000 units of lithium to cover its costs.
Step 3: Interpret the Results
- Market Opportunities: Consider if the sales targets are realistic. Is there strong demand for lithium? Is the price competitive?
- Strategic Decisions: If the break-even point is deemed too high, strategies like cost-cutting, price adjustments, or marketing initiatives could be developed to boost profitability.
Break-Even Analysis for Low Profitability
Another important use of break-even analysis is identifying causes of low profitability. Imagine your client is experiencing increasing losses, despite rising revenue. In such a case, the analysis could show that rising costs from a newly opened factory are the cause. If the additional fixed costs are higher than the revenue growth, it leads to losses. Before recommending marketing measures, you should check the break-even number of units sold. For the analysis, you’ll need the following info:
- Annual Fixed Costs: €50 million
- Average Variable Cost per Product: €1,000
- Average Product Price: €1,500
The profit per product calculation would be:
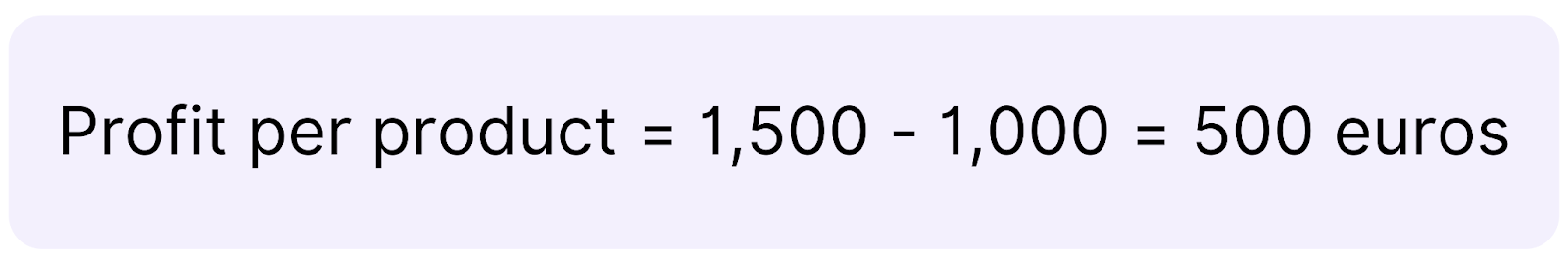
To find the break-even point, use:
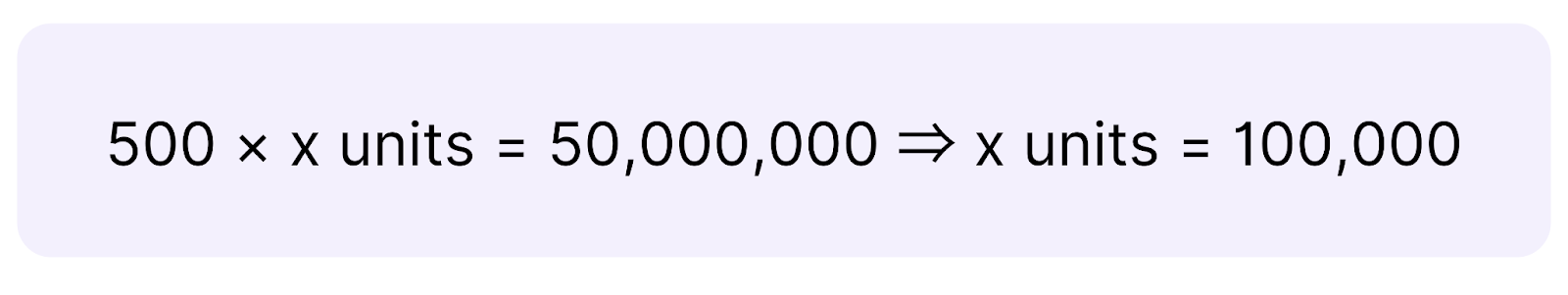
The company would need to produce and sell 100,000 units. If this isn’t feasible, you might recommend selling the new factory.
Key Takeaways 💡
The break-even analysis helps you understand your client’s profitability and make informed decisions. By carefully analyzing fixed and variable costs and determining the break-even point, you can develop strategies to boost revenue and minimize risk.
Remember, though, that every business is unique. It’s essential to adapt the analysis to each situation.
During a case interview, think about how to increase profitability and optimize the cost structure. Use the break-even analysis as your guiding tool to gain insights for your clients and help them overcome their business challenges successfully.
Find more key calculations like ROI and ROAS or balance sheet analysis that you can practice for your case interview on PrepLounge.