McK case math

Question

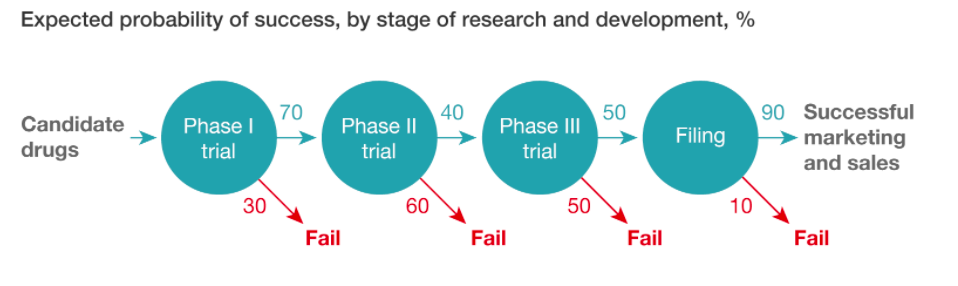
GlobaPharm (the client) believes that the likelihood of success of the new drug candidate can be improved by investing an additional $150 million in a larger Phase II trial. The hope is that this investment would raise the success rate in Phase II, meaning that more candidate drugs successfully make it to Phase III and beyond. By how much would the Phase II success rate need to increase in order for this investment to break even? assume that if the drug is successfully marketed and sold, it would be worth $1.2 billion (that is, the present value of all future profits from selling the drug is $1.2 billion).

Answer: Probability of success should increase by 40 percentage point (i.e change from 40% currently, to 80% )

How can you get this answer? I didn't find the solution very intuitive to follow.

Answer 1

Hi,

Thanks for your question. I do not have the full case, so correct me if I'm missing something. I'll try to make it as simple as possible. It's basically a betting game.

- Currently ~1 in 8 candidate drug goes to market (70%*40%*50%*90%=12.6% ie ~1/8) which means that on every drug candidate we make an “expected winning” or average winning of ~150M (1.2B divided by 8). If I take a portfolio of 8 drugs, I know that 1 will make it to the market and I will get 1.2B from that drug. So on average, one drug gives me 150M

- If the company invests an additional 150M, we need to have at least 150M in additional “expected winning” to breakeven. Since we already have an “expected winning” of 150M, we basically want to double that winning.

- To double the winning we either double the future profits from the drug candidate (which seems to be out of scope) or we double the likelihood of winning, ie we double the number of drugs that make it to the market

- Since we can only impact Phase 2 here, we have to double the likelihood on Phase 2 ie move from 40% to 80% which is 40pp more

I hope this helps, let me know if it's unclear. And let me know if you want to practice similar questions.

Best,

Mehdi

Answer 2

Current EV (expected value) = 70%*40%*50%*90%*1200 = 150

Additional Invesment = 150M

Additional Investment / EV = 150/150 = 1 = 100%

Expected Value should increase by 100%

Current success Phase II: 40%.

New success rate Phase II = (1+100%)*40%=2*40%=80%

Answer 3

Hi there,

I remember when I first got a question like this in my initial case prep - I was equally confused!

Remember here that each stage has its own independent probability of success.

Therefore, any changes to Phase II also have to include calculations for Phase III and Filing.