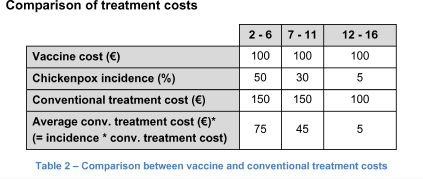
Beyer, one of the biggest pharmaceutical companies in the world, just invented a very reliable vaccine against Chickenpox, a disease that affects children in the age from 2 to 16 years.
Beyer came to you wondering what their potential sales in Europe in the first year would be if they launched this product next year. They are only interested in the overall sales revenue as they already know that the vaccine can be sold for a profit. This is more meant to show them how big the volume they have to supply is and what the revenue would be.
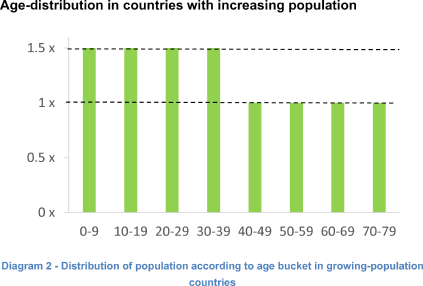
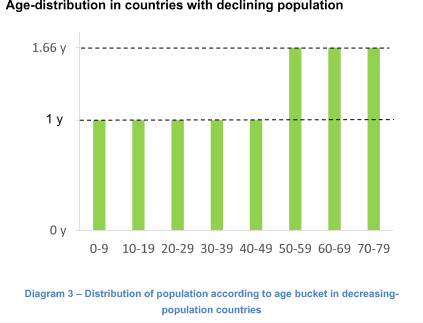
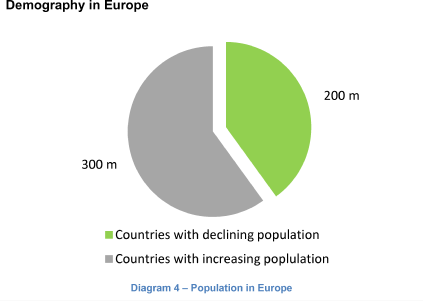
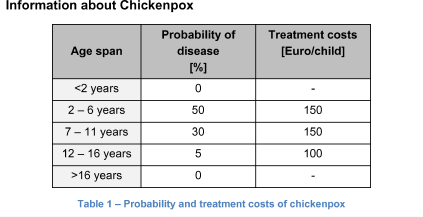












Children vaccine
i