Kapitalwert (Net Present Value, kurz NPV) - Definition, Beispiele und Berechnungsweise
Definition des Kapitalwerts (NPV)
Mit dem Kapitalwert (NPV) kannst Du zukünftige Cashflows auf der Grundlage des Barwerts bewerten. Er ist die Summe der Barwerte des Geldes zu verschiedenen zukünftigen Zeitpunkten. Der Barwert (Present Value, kurz PV) bestimmt, wie viel zukünftiges Geld heute wert ist. Auf der Grundlage des Kapitalwerts können wir eine Reihe von Projekten/Investitionen mit unterschiedlichen Cashflows im Zeitverlauf vergleichen. Auf diese Weise können wir die Attraktivität eines Unternehmens quantitativ bewerten, indem wir die Kapitalwerte miteinander vergleichen.
Zeitwert des Geldes - eine intuitive und finanzielle Erklärung
Je näher die zukünftigen Cashflows an der Gegenwart liegen, desto wertvoller ist Dein Geld. Dieses Konzept wird auch als Zeitwert des Geldes bezeichnet und wir geben im Folgenden zwei Erklärungen:
- Eine intuitive Erklärung: Die Menschen bevorzugen Geld in der Gegenwart aufgrund ihrer Risikoaversion. Hättest Du lieber heute oder in einem Jahr 100 Dollar? Offensichtlich heute, denn es besteht das Risiko, dass Du die 100 Dollar in einem Jahr nicht mehr bekommst. Wenn du das Geld hast, musst Du Dich außerdem entscheiden, ob Du es sofort ausgibst oder damit wartest, es auszugeben.
- Eine finanzielle Erklärung: Stell Dir vor, Du hast $100. Wie viel ist es in einem Jahr wert? Wenn Du das Geld nicht in der Tasche lässt, hast Du in der Regel die Möglichkeit, das Geld mit geringem und fast vernachlässigbarem Risiko auf Dein Bankkonto zu legen. Du erhältst zwar Zinsen, kannst aber durch die Inflation an Wert verlieren. Der inflationsbereinigte Zinssatz kann jedoch 2 % betragen, in absoluten Zahlen $2. Insgesamt sind Deine $100 nach einem Jahr $102 wert. Jetzt kannst Du rückwärts rechnen: Wenn Du in einem Jahr einen Endwert von $102 hast, wie viel ist er dann heute wert? Es sind $102 geteilt durch $102 was wieder $100 ergibt.
So berechnest Du den Kapitalwert (NPV)
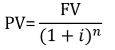
- PV ist der aktuelle Barwert
- FV (Future Value) ist der zukünftige Endwert
- i ist der Dezimalwert des Zinssatzes für eine bestimmte Periode
- n ist die Anzahl der Perioden zwischen Gegenwart und Zukunft
Im Folgenden findest Du die Berechnung des obigen PV-Beispiels mit einem zukünftigen Endwert von $102 und einem Zinssatz von 2 %,
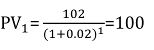
Nachfolgend findest Du eine leicht abgewandelte Version des obigen Beispiels, in der Du $102 in zwei Jahren statt im nächsten Jahr erhältst. Die zweijährige Investition bringt Dir zweimal einen theoretischen Zins ein, weshalb Du zweimal diskontierst.
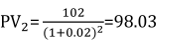
Der Kapitalwert dieser beiden Zahlungen von $102 in einem und zwei Jahren ist einfach die Summe.
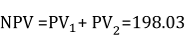
Wende die Kapitalwertkürzel an, um in Case-Situationen erfolgreich zu sein
Es ist unwahrscheinlich, dass Du während eines Case-Interviews einen komplexen Kapitalwert berechnen musst, weil die Berechnungen sonst zu kompliziert werden. Aber in manchen Fällen kannst Du einige Abkürzungen anwenden, wie unten beschrieben:
1. Ewigkeit: der Kapitalwert für unendliche Cashflows (d.h. das Unternehmen wird über einen unendlichen Zeitraum hinweg Gewinne erwirtschaften)
Für unendliche Cashflows gibt es eine vereinfachte Formel:
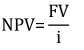
Stell Dir vor, Du sollst in einem Case-Interview ein Unternehmen bewerten. Ein gängiger Ansatz ist, den Wert eines Unternehmens als die Summe aller abgezinsten zukünftigen Gewinne zu definieren. Wenn Du davon ausgehst, dass ein Unternehmen für einen unbestimmten Zeithorizont jedes Jahr die gleichen Gewinne erzielt, teilst Du einfach den zukünftigen Wert aller Gewinne durch den jeweiligen Abzinsungssatz. Wenn Du z. B. erwartest, dass das Unternehmen jedes Jahr 100 US-Dollar einbringt, ist es 2500 US-Dollar wert (bei einem Abzinsungssatz von 4 %).
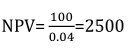
Um das Ganze pragmatischer zu gestalten, könntest Du davon ausgehen, dass die Gewinne des Unternehmens jedes Jahr mit einer bestimmten Rate g wachsen werden.
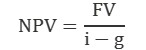
Besonders bei kurzfristigen Zeithorizonten ist es schwierig, das erwartete Wachstum zu bestimmen. Eine ungefähre Wachstumsrate für Gewinne, die weit in der Zukunft liegen, liegt oft bei etwa 2%. Nach einer gewissen Zeit endet jeder Geschäfts- oder Produktlebenszyklus in einem wettbewerbsorientierten Marktumfeld und wächst einfach mit der gleichen Rate wie die Gesamtwirtschaft. Das obige Beispiel, das mit einer kontinuierlichen Wachstumsrate von 2 % neu berechnet wurde, ergibt einen Kapitalwert von $5000 für das Unternehmen.
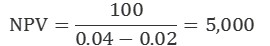
Beachte, dass der Wert im Vergleich zu den Berechnungen ohne Wachstum doppelt so hoch ist. Kapitalwertberechnungen reagieren sehr empfindlich auf Änderungen der Inputs. Deshalb wird in den meisten Fällen eine Sensitivitätsanalyse durchgeführt. Dazu musst Du eine Reihe möglicher Kapitalwerte erstellen, indem Du eine Reihe möglicher Wachstums- und Abzinsungssätze verwendest.
2. Finde den richtigen Zinssatz
Den richtigen Abzinsungsfaktor für die Kapitalwertberechnung zu finden, ist die Aufgabe ganzer Bankabteilungen. Im Allgemeinen gibt es eine Grundregel: Je größer das Risiko, desto höher der Abzinsungssatz.
Der Grundgedanke hinter dieser Regel ist einfach: Je weniger Du Dir sicher sein kannst, zukünftige Erträge zu erhalten, desto geringer ist ihr Wert. Wenn Du den Abzinsungssatz erhöhst, schrumpft der Kapitalwert der künftigen Erträge. Die Abzinsungssätze für relativ sichere Geldströme liegen zwischen 1 % und 3 %, aber für die meisten Unternehmen verwendest Du einen Abzinsungssatz zwischen 4 % und 10 %, und für spekulative Start-up-Investitionen kann der angewandte Zinssatz bis zu 40 % betragen. In Case-Interviews kannst Du direkt nach dem Diskontierungssatz fragen oder ihn für die meisten Szenarien auf 10% schätzen, wenn der Interviewer Dich bittet, ihn zu schätzen.
Warum wird der Kapitalwert von Unternehmen verwendet?
Der Kapitalwert ist ein starker Indikator für Unternehmen, um festzustellen, ob ein Projekt rentabel ist oder nicht. Da er den Zinssatz und die Inflationsrate (die in der Regel gleich hoch sind) berücksichtigt, kann der reale Wert des Geldes in jedem Jahr des Projekts betrachtet werden. Wenn der berechnete Kapitalwert positiv ist, kann das Unternehmen argumentieren, dass das Projekt oder die Investition rentabel ist, da die erwirtschafteten Erträge die Kosten übersteigen, und zwar im Barwert in Form von Dollar. Ist der berechnete Kapitalwert hingegen negativ, ist dies ein Indikator dafür, dass ein Unternehmen von einer Investition oder einem Projekt Abstand nehmen sollte, da es zu einem Nettoverlust führt. Der Kapitalwert kann also ein wertvolles Instrument für Unternehmen sein, um zu beurteilen, ob sie in ein Projekt investieren sollten oder nicht.
Vorteile des Kapitalwerts (NPV)
Der Kapitalwert (NPV) bietet viele Vorteile, die sich alle auf die Genauigkeit der Berechnung beziehen, mit der der tatsächliche Wert eines zukünftigen Geldbetrags unter den gegenwärtigen Bedingungen ermittelt wird. Die Messung basiert auf der Zeitwerttheorie des Geldes, die besagt, dass ein bestimmter Geldbetrag heute mehr wert ist als der gleiche Geldbetrag in der Zukunft. Die Inflationsraten und die Raten, mit denen investiertes Geld in der Zukunft wachsen kann, ergeben zusammen einen Diskontsatz, der zukünftiges Geld abwertet. Da der Abzinsungssatz bei der Berechnung berücksichtigt wird, ist einer der Hauptvorteile des Kapitalwerts, dass er wichtige finanzielle Entscheidungen ermöglicht. Geschäftsentscheidungen sind in jeder Größenordnung schwierig zu treffen, von der Entscheidung über eine wichtige Anschaffung bis hin zur Entscheidung über ein kostspieliges neues Projekt. Es kann töricht sein, diese Entscheidungen zu treffen, ohne vorher die Auswirkungen von Zeit auf Geld zu berücksichtigen. Aus diesem Grund ist eine Berechnung, die das Verhältnis zwischen Zeit und Geld berücksichtigt, einer der Hauptvorteile des Kapitalwerts, von entscheidender Bedeutung.
Der vielleicht wichtigste Vorteil des Barwerts ist seine Nützlichkeit für eine Geschäftsentscheidung.
Sobald der Kapitalwert berechnet ist, muss das Unternehmen, das die Entscheidung trifft, nur noch die aktuellen Kosten mit dem Kapitalwert vergleichen. Ein Unternehmen, das zum Beispiel die Möglichkeit hat, eine neue Fabrik für 100.000 USD zu kaufen, sollte nur dann mit dem Kauf fortfahren, wenn der Kapitalwert der zukünftigen Cashflows größer als 100.000 USD ist. Andernfalls wäre es für das Unternehmen besser, das Geld anderweitig zu investieren.
Die Grenzen des Kapitalwerts
In der Praxis ist das Konzept des Kapitalwerts weit verbreitet und wird häufig verwendet. Dennoch gibt es Nachteile und Einschränkungen dieser Kennzahl. Zum Beispiel basiert der berechnete Wert auf verschiedenen Annahmen. Wenn eine oder mehrere Annahmen in der Praxis nicht eintreten, können der Kapitalwert und der tatsächliche Nutzen einer Investition voneinander abweichen. Gleichzeitig ist das Konzept anfällig für die Beeinflussung durch den Bewerter. Einzelne Annahmen können theoretisch so lange geändert werden, bis das Ergebnis mit den Erwartungen des Bewerters übereinstimmt. Daher hat der Kapitalwert die höchste Aussagekraft, wenn ein Investor ihn selbst berechnet.
Beispiel: Ein Unternehmen prüft den Nutzen der Investition in einer neue Produktionslinie. Das Unternehmen geht davon aus, dass die Maschine zehn Jahre lang genutzt wird und plant daher mit zehn Perioden, um den Kapitalwert zu ermitteln. Nach sieben Jahren fragen die Kunden das produzierte Produkt jedoch nicht mehr nach. Die Produktionsanlage muss zugunsten einer neuen Maschine ausrangiert werden. Der ursprünglich berechnete Kapitalwert ist aufgrund der geänderten Nutzungsdauer deutlich niedriger als ursprünglich angenommen.
Obwohl der Kapitalwert ein umfassendes Konzept ist, werden die Sekundäreffekte einer Investition nicht berücksichtigt. Die verwendete Cashflow-Reihe bezieht sich direkt auf die untersuchte Investition. Der Kapitalwert kann keine Synergieeffekte in anderen Unternehmensteilen oder z.B. ein verbessertes Unternehmensimage messen.
Die wichtigsten Schlussfolgerungen
- Nutze den Kapitalwert, um künftige Cashflows im heutigen Zeitwert des Geldes zu bewerten
- Du kannst verschiedene Investitionen quantitativ vergleichen, indem Du risikoadjustierte Kapitalwerte berechnest
- Kapitalwerte werden verwendet, um ein Unternehmen auf der Grundlage seiner zukünftigen Gewinne zu bewerten
- Der Kapitalwert berücksichtigt nicht die Sekundäreffekte einer Investition

